Truncated 120-cells
 120-cell |
 Truncated 120-cell |
 Rectified 120-cell |
 Bitruncated 120-cell Bitruncated 600-cell |
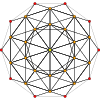 600-cell |
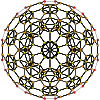 Truncated 600-cell |
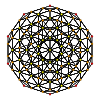 Rectified 600-cell | |
| Orthogonal projections in H3 Coxeter plane | |||
|---|---|---|---|
In geometry, a truncated 120-cell is a uniform 4-polytope formed as the truncation of the regular 120-cell.
There are three truncations, including a bitruncation, and a tritruncation, which creates the truncated 600-cell.
Truncated 120-cell
[edit]| Truncated 120-cell | |
|---|---|
 Schlegel diagram (tetrahedron cells visible) | |
| Type | Uniform 4-polytope |
| Uniform index | 36 |
| Schläfli symbol | t0,1{5,3,3} or t{5,3,3} |
| Coxeter diagrams | |
| Cells | 600 3.3.3 120 3.10.10 |
| Faces | 2400 triangles 720 decagons |
| Edges | 4800 |
| Vertices | 2400 |
| Vertex figure |  triangular pyramid |
| Dual | Tetrakis 600-cell |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |

The truncated 120-cell or truncated hecatonicosachoron is a uniform 4-polytope, constructed by a uniform truncation of the regular 120-cell 4-polytope.
It is made of 120 truncated dodecahedral and 600 tetrahedral cells. It has 3120 faces: 2400 being triangles and 720 being decagons. There are 4800 edges of two types: 3600 shared by three truncated dodecahedra and 1200 are shared by two truncated dodecahedra and one tetrahedron. Each vertex has 3 truncated dodecahedra and one tetrahedron around it. Its vertex figure is an equilateral triangular pyramid.
Alternate names
[edit]- Truncated 120-cell (Norman W. Johnson)
- Tuncated hecatonicosachoron / Truncated dodecacontachoron / Truncated polydodecahedron
- Truncated-icosahedral hexacosihecatonicosachoron (Acronym thi) (George Olshevsky, and Jonathan Bowers)[1]
Images
[edit]| H4 | - | F4 |
|---|---|---|
 [30] |
 [20] |
 [12] |
| H3 | A2 | A3 |
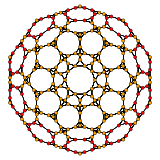 [10] |
 [6] |
 [4] |
 net |
 Central part of stereographic projection (centered on truncated dodecahedron) |
 Stereographic projection |
Bitruncated 120-cell
[edit]| Bitruncated 120-cell | ||
|---|---|---|
 Schlegel diagram, centered on truncated icosahedron, truncated tetrahedral cells visible | ||
| Type | Uniform 4-polytope | |
| Uniform index | 39 | |
| Coxeter diagram | ||
| Schläfli symbol | t1,2{5,3,3} or 2t{5,3,3} | |
| Cells | 720: 120 5.6.6 600 3.6.6 | |
| Faces | 4320: 1200{3}+720{5}+ 2400{6} | |
| Edges | 7200 | |
| Vertices | 3600 | |
| Vertex figure |  digonal disphenoid | |
| Symmetry group | H4, [3,3,5], order 14400 | |
| Properties | convex, vertex-transitive | |

The bitruncated 120-cell or hexacosihecatonicosachoron is a uniform 4-polytope. It has 720 cells: 120 truncated icosahedra, and 600 truncated tetrahedra. Its vertex figure is a digonal disphenoid, with two truncated icosahedra and two truncated tetrahedra around it.
Alternate names
[edit]- Bitruncated 120-cell / Bitruncated 600-cell (Norman W. Johnson)
- Bitruncated hecatonicosachoron / Bitruncated hexacosichoron / Bitruncated polydodecahedron / Bitruncated polytetrahedron
- Truncated-icosahedral hexacosihecatonicosachoron (Acronym Xhi) (George Olshevsky, and Jonathan Bowers)[2]
Images
[edit] Stereographic projection (Close up) |
| H3 | A2 / B3 / D4 | A3 / B2 / D3 |
|---|---|---|
 [10] |
 [6] |
 [4] |
Truncated 600-cell
[edit]| Truncated 600-cell | |
|---|---|
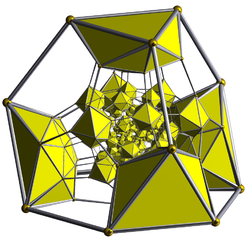 Schlegel diagram (icosahedral cells visible) | |
| Type | Uniform 4-polytope |
| Uniform index | 41 |
| Schläfli symbol | t0,1{3,3,5} or t{3,3,5} |
| Coxeter diagram | |
| Cells | 720: 120 600 |
| Faces | 2400{3}+1200{6} |
| Edges | 4320 |
| Vertices | 1440 |
| Vertex figure |  pentagonal pyramid |
| Dual | Dodecakis 120-cell |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |

The truncated 600-cell or truncated hexacosichoron is a uniform 4-polytope. It is derived from the 600-cell by truncation. It has 720 cells: 120 icosahedra and 600 truncated tetrahedra. Its vertex figure is a pentagonal pyramid, with one icosahedron on the base, and 5 truncated tetrahedra around the sides.
Alternate names
[edit]- Truncated 600-cell (Norman W. Johnson)
- Truncated hexacosichoron (Acronym tex) (George Olshevsky, and Jonathan Bowers)[3]
- Truncated tetraplex (Conway)
Structure
[edit]The truncated 600-cell consists of 600 truncated tetrahedra and 120 icosahedra. The truncated tetrahedral cells are joined to each other via their hexagonal faces, and to the icosahedral cells via their triangular faces. Each icosahedron is surrounded by 20 truncated tetrahedra.
Images
[edit] Centered on icosahedron |
 Centered on truncated tetrahedron |
 Central part and some of 120 red icosahedra. |
 Net |
| H4 | - | F4 |
|---|---|---|
 [30] |
 [20] |
 [12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] |
 [6] |
 [4] |
Related polytopes
[edit]| H4 family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 120-cell | rectified 120-cell |
truncated 120-cell |
cantellated 120-cell |
runcinated 120-cell |
cantitruncated 120-cell |
runcitruncated 120-cell |
omnitruncated 120-cell | ||||
| {5,3,3} | r{5,3,3} | t{5,3,3} | rr{5,3,3} | t0,3{5,3,3} | tr{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} | ||||

|

|

|
|
|
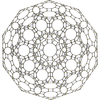
|

|

| ||||

|

|

|

|
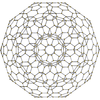
|
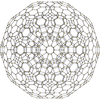
|
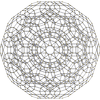
| |||||
| 600-cell | rectified 600-cell |
truncated 600-cell |
cantellated 600-cell |
bitruncated 600-cell |
cantitruncated 600-cell |
runcitruncated 600-cell |
omnitruncated 600-cell | ||||
| {3,3,5} | r{3,3,5} | t{3,3,5} | rr{3,3,5} | 2t{3,3,5} | tr{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} | ||||
Notes
[edit]References
[edit]- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [1] m58 m59 m53
- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 36, 39, 41, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora)". o3o3x5x - thi, o3x3x5o - xhi, x3x3o5o - tex
- Four-Dimensional Polytope Projection Barn Raisings (A Zometool construction of the truncated 120-cell), George W. Hart

