Interstitial site

In crystallography, interstitial sites, holes or voids are the empty space that exists between the packing of atoms (spheres) in the crystal structure.[citation needed]
The holes are easy to see if you try to pack circles together; no matter how close you get them or how you arrange them, you will have empty space in between. The same is true in a unit cell; no matter how the atoms are arranged, there will be interstitial sites present between the atoms. These sites or holes can be filled with other atoms (interstitial defect). The picture with packed circles is only a 2D representation. In a crystal lattice, the atoms (spheres) would be packed in a 3D arrangement. This results in different shaped interstitial sites depending on the arrangement of the atoms in the lattice.
Close packed
[edit]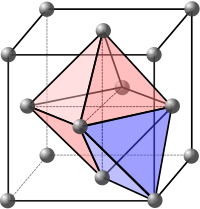
A close packed unit cell, both face-centered cubic and hexagonal close packed, can form two different shaped holes. Looking at the three green spheres in the hexagonal packing illustration at the top of the page, they form a triangle-shaped hole. If an atom is arranged on top of this triangular hole it forms a tetrahedral interstitial hole. If the three atoms in the layer above are rotated and their triangular hole sits on top of this one, it forms an octahedral interstitial hole.[citation needed] In a close-packed structure there are 4 atoms per unit cell and it will have 4 octahedral voids (1:1 ratio) and 8 tetrahedral voids (1:2 ratio) per unit cell.[1] The tetrahedral void is smaller in size and could fit an atom with a radius 0.225 times the size of the atoms making up the lattice. An octahedral void could fit an atom with a radius 0.414 times the size of the atoms making up the lattice.[1] An atom that fills this empty space could be larger than this ideal radius ratio, which would lead to a distorted lattice due to pushing out the surrounding atoms, but it cannot be smaller than this ratio.[1]
Face-centered cubic (FCC)
[edit]If half of the tetrahedral sites of the parent FCC lattice are filled by ions of opposite charge, the structure formed is the zincblende crystal structure. If all the tetrahedral sites of the parent FCC lattice are filled by ions of opposite charge, the structure formed is the fluorite structure or antifluorite structure. If all the octahedral sites of the parent FCC lattice are filled by ions of opposite charge, the structure formed is the rock-salt structure.
Hexagonal close packed (HCP)
[edit]If half of the tetrahedral sites of the parent HCP lattice are filled by ions of opposite charge, the structure formed is the wurtzite crystal structure. If all the octahedral sites of the anion HCP lattice are filled by cations, the structure formed is the nickel arsenide structure.
Simple cubic
[edit]A simple cubic unit cell, with stacks of atoms arranged as if at the eight corners of a cube would form a single cubic hole or void in the center. If these voids are occupied by ions of opposite charge from the parent lattice, the cesium chloride structure is formed.
Body-centered cubic (BCC)
[edit]A body-centered cubic unit cell has six octahedral voids located at the center of each face of the unit cell, and twelve further ones located at the midpoint of each edge of the same cell, for a total of six net octahedral voids. Additionally, there are 24 tetrahedral voids located in a square spacing around each octahedral void, for a total of twelve net tetrahedral voids. These tetrahedral voids are not local maxima and are not technically voids, but they do occasionally appear in multi-atom unit cells.
Interstitial defect
[edit]An interstitial defect refers to additional atoms occupying some interstitial sites at random as crystallographic defects in a crystal which normally has empty interstitial sites by default.
References
[edit]- ^ a b c "Study of Interstitial Voids". Archived from the original on 2020-08-04.
