Dihedral symmetry in three dimensions

Selected point groups in three dimensions
Polyhedral group, [n,3], (*n32)
Involutional symmetry C_s, (*) [ ] =	Cyclic symmetry C_nv, (*nn) [n] =	Dihedral symmetry D_nh, (*n22) [n,2] =
Tetrahedral symmetry T_d, (*332) [3,3] =	Octahedral symmetry O_h, (*432) [4,3] =	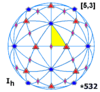Icosahedral symmetry I_h, (*532) [5,3] =

In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dih_n (for n ≥ 2).

Types

There are 3 types of dihedral symmetry in three dimensions, each shown below in 3 notations: Schönflies notation, Coxeter notation, and orbifold notation.

Chiral

D_n, [n,2]⁺, (22n) of order 2n – dihedral symmetry or para-n-gonal group (abstract group: Dih_n).

Achiral

D_nh, [n,2], (*22n) of order 4n – prismatic symmetry or full ortho-n-gonal group (abstract group: Dih_n × Z₂).
D_nd (or D_nv), [2n,2⁺], (2*n) of order 4n – antiprismatic symmetry or full gyro-n-gonal group (abstract group: Dih_2n).

For a given n, all three have n-fold rotational symmetry about one axis (rotation by an angle of 360°/n does not change the object), and 2-fold rotational symmetry about a perpendicular axis, hence about n of those. For n = ∞, they correspond to three Frieze groups. Schönflies notation is used, with Coxeter notation in brackets, and orbifold notation in parentheses. The term horizontal (h) is used with respect to a vertical axis of rotation.

In 2D, the symmetry group D_n includes reflections in lines. When the 2D plane is embedded horizontally in a 3D space, such a reflection can either be viewed as the restriction to that plane of a reflection through a vertical plane, or as the restriction to the plane of a rotation about the reflection line, by 180°. In 3D, the two operations are distinguished: the group D_n contains rotations only, not reflections. The other group is pyramidal symmetry C_nv of the same order, 2n.

With reflection symmetry in a plane perpendicular to the n-fold rotation axis, we have D_nh, [n], (*22n).

D_nd (or D_nv), [2n,2⁺], (2*n) has vertical mirror planes between the horizontal rotation axes, not through them. As a result, the vertical axis is a 2n-fold rotoreflection axis.

D_nh is the symmetry group for a regular n-sided prism and also for a regular n-sided bipyramid. D_nd is the symmetry group for a regular n-sided antiprism, and also for a regular n-sided trapezohedron. D_n is the symmetry group of a partially rotated prism.

n = 1 is not included because the three symmetries are equal to other ones:

D₁ and C₂: group of order 2 with a single 180° rotation.
D_1h and C_2v: group of order 4 with a reflection in a plane and a 180° rotation about a line in that plane.
D_1d and C_2h: group of order 4 with a reflection in a plane and a 180° rotation about a line perpendicular to that plane.

For n = 2 there is not one main axis and two additional axes, but there are three equivalent ones.

D₂, [2,2]⁺, (222) of order 4 is one of the three symmetry group types with the Klein four-group as abstract group. It has three perpendicular 2-fold rotation axes. It is the symmetry group of a cuboid with an S written on two opposite faces, in the same orientation.
D_2h, [2,2], (*222) of order 8 is the symmetry group of a cuboid.
D_2d, [4,2⁺], (2*2) of order 8 is the symmetry group of e.g.:
- A square cuboid with a diagonal drawn on one square face, and a perpendicular diagonal on the other one.
- A regular tetrahedron scaled in the direction of a line connecting the midpoints of two opposite edges (D_2d is a subgroup of T_d; by scaling, we reduce the symmetry).

Subgroups

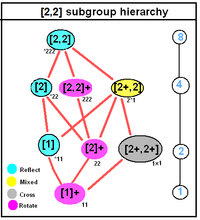D_2h, [2,2], (*222)	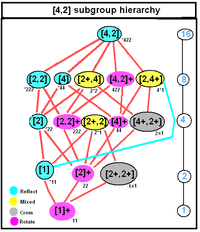D_4h, [4,2], (*224)

For D_nh, [n,2], (*22n), order 4n

C_nh, [n⁺,2], (n*), order 2n
C_nv, [n,1], (*nn), order 2n
D_n, [n,2]⁺, (22n), order 2n

For D_nd, [2n,2⁺], (2*n), order 4n

S_2n, [2n⁺,2⁺], (n×), order 2n
C_nv, [n⁺,2], (n*), order 2n
D_n, [n,2]⁺, (22n), order 2n

D_nd is also subgroup of D_2nh.

Examples

D_2h, [2,2], (*222) Order 8	D_2d, [4,2⁺], (2*2) Order 8	D_3h, [3,2], (*223) Order 12
basketball seam paths	baseball seam paths (ignoring directionality of seam)	Beach ball (ignoring colors)

D_nh, [n], (*22n):

prisms

D_5h, [5], (*225):

Pentagrammic prism	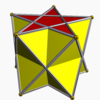Pentagrammic antiprism

D_4d, [8,2⁺], (2*4):

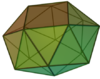Snub square antiprism

D_5d, [10,2⁺], (2*5):

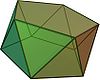Pentagonal antiprism	Pentagrammic crossed-antiprism	pentagonal trapezohedron

D_17d, [34,2⁺], (2*17):

Heptadecagonal antiprism

References

Coxeter, H. S. M. and Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.{{cite book}}: CS1 maint: multiple names: authors list (link)
N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.5 Spherical Coxeter groups
Conway, John Horton; Huson, Daniel H. (2002), "The Orbifold Notation for Two-Dimensional Groups", Structural Chemistry, 13 (3), Springer Netherlands: 247–257, doi:10.1023/A:1015851621002, S2CID 33947139

External links

Graphic overview of the 32 crystallographic point groups – form the first parts (apart from skipping n=5) of the 7 infinite series and 5 of the 7 separate 3D point groups

Types

Subgroups

Examples

See also

References

External links