Guyou hemisphere-in-a-square projection

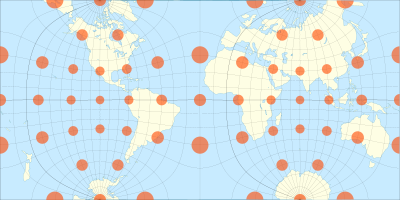
The Guyou hemisphere-in-a-square projection is a conformal map projection for the hemisphere. It is an oblique aspect of the Peirce quincuncial projection.
History
[edit]The projection was developed by Émile Guyou of France in 1887.[1][2]
Formal description
[edit]The projection can be computed as an oblique aspect of the Peirce quincuncial projection by rotating the axis 45 degrees. It can also be computed by rotating the coordinates −45 degrees before computing the stereographic projection; this projection is then remapped into a square whose coordinates are then rotated 45 degrees.[3]
The projection is conformal except for the four corners of each hemisphere's square. Like other conformal polygonal projections, the Guyou is a Schwarz–Christoffel mapping.
Properties
[edit]Its properties are very similar to those of the Peirce quincuncial projection:
- Each hemisphere is represented as a square, the sphere as a rectangle of aspect ratio 2:1.
- The part where the exaggeration of scale amounts to double that at the centre of each square is only 9% of the area of the sphere, against 13% for the Mercator and 50% for the stereographic[4]
- The curvature of lines representing great circles is, in every case, very slight, over the greater part of their length.[4]
- It is conformal everywhere except at the corners of the square that corresponds to each hemisphere, where two meridians change direction abruptly twice each; the Equator is represented by a horizontal line.
- It can be tessellated in all directions.
Related projections
[edit]- The Adams hemisphere-in-a-square projection and the Peirce quincuncial projection are different aspects of the same underlying Schwarz–Christoffel mapping. Such mappings are transformations of half a stereographic projection.
See also
[edit]References
[edit]- ^ E. Guyou (1887) "Nouveau système de projection de la sphère: Généralisation de la projection de Mercator", Annales Hydrographiques, Ser. 2, Vol. 9, 16–35. https://www.retronews.fr/journal/annales-hydrographiques/1-janvier-1887/1877/4868382/23
- ^ Snyder, John P. (1993). Flattening the Earth. University of Chicago. ISBN 0-226-76746-9.
- ^ Lee, L. P. (1976). Conformal Projections Based on Elliptic Functions. Cartographica Monographs. Vol. 16. Toronto: B. V. Gutsell, York University. ISBN 0-919870-16-3. Supplement No. 1 to The Canadian Cartographer 13.
- ^ a b C.S. Peirce (December 1879). "A Quincuncial Projection of the Sphere". American Journal of Mathematics. 2 (4). The Johns Hopkins University Press: 394–396. doi:10.2307/2369491. JSTOR 2369491.
