Polygon triangulation
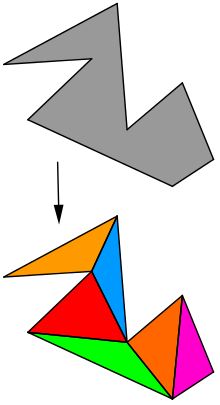
In computational geometry, polygon triangulation is the partition of a polygonal area (simple polygon) P into a set of triangles,[1] i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.
Triangulations may be viewed as special cases of planar straight-line graphs. When there are no holes or added points, triangulations form maximal outerplanar graphs.
Polygon triangulation without extra vertices
[edit]Over time, a number of algorithms have been proposed to triangulate a polygon.
Special cases
[edit]
It is trivial to triangulate any convex polygon in linear time into a fan triangulation, by adding diagonals from one vertex to all other non-nearest neighbor vertices.
The total number of ways to triangulate a convex n-gon by non-intersecting diagonals is the (n−2)nd Catalan number, which equals
- ,
a formula found by Leonhard Euler.[2]
A monotone polygon can be triangulated in linear time with either the algorithm of A. Fournier and D.Y. Montuno,[3] or the algorithm of Godfried Toussaint.[4]
Ear clipping method
[edit]
One way to triangulate a simple polygon is based on the two ears theorem, as the fact that any simple polygon with at least 4 vertices without holes has at least two "ears", which are triangles with two sides being the edges of the polygon and the third one completely inside it.[5] The algorithm then consists of finding such an ear, removing it from the polygon (which results in a new polygon that still meets the conditions) and repeating until there is only one triangle left.
This algorithm is easy to implement, but slower than some other algorithms, and it only works on polygons without holes. An implementation that keeps separate lists of convex and concave vertices will run in O(n2) time. This method is known as ear clipping and sometimes ear trimming. An efficient algorithm for cutting off ears was discovered by Hossam ElGindy, Hazel Everett, and Godfried Toussaint.[6]
Monotone polygon triangulation
[edit]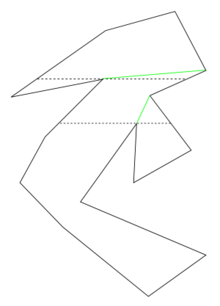
A simple polygon is monotone with respect to a line L, if any line orthogonal to L intersects the polygon at most twice. A monotone polygon can be split into two monotone chains. A polygon that is monotone with respect to the y-axis is called y-monotone. A monotone polygon with n vertices can be triangulated in O(n) time. Assuming a given polygon is y-monotone, the greedy algorithm begins by walking on one chain of the polygon from top to bottom while adding diagonals whenever it is possible.[1] It is easy to see that the algorithm can be applied to any monotone polygon.
Triangulating a non-monotone polygon
[edit]If a polygon is not monotone, it can be partitioned into monotone subpolygons in O(n log n) time using a sweep-line approach. The algorithm does not require the polygon to be simple, thus it can be applied to polygons with holes. Generally, this algorithm can triangulate a planar subdivision with n vertices in O(n log n) time using O(n) space.[1]
Dual graph of a triangulation
[edit]A useful graph that is often associated with a triangulation of a polygon P is the dual graph. Given a triangulation TP of P, one defines the graph G(TP) as the graph whose vertex set are the triangles of TP, two vertices (triangles) being adjacent if and only if they share a diagonal. It is easy to observe that G(TP) is a tree with maximum degree 3.
Computational complexity
[edit]Until 1988, whether a simple polygon can be triangulated faster than O(n log n) time was an open problem in computational geometry.[1] Then, Tarjan & Van Wyk (1988) discovered an O(n log log n)-time algorithm for triangulation,[7] later simplified by Kirkpatrick, Klawe & Tarjan (1992).[8] Several improved methods with complexity O(n log* n) (in practice, indistinguishable from linear time) followed.[9][10][11]
Bernard Chazelle showed in 1991 that any simple polygon can be triangulated in linear time, though the proposed algorithm is very complex.[12] A simpler randomized algorithm with linear expected time is also known.[13]
Seidel's decomposition algorithm[10] and Chazelle's triangulation method are discussed in detail in Li & Klette (2011).[14]
The time complexity of triangulation of an n-vertex polygon with holes has an Ω(n log n) lower bound, in algebraic computation tree models of computation.[1] It is possible to compute the number of distinct triangulations of a simple polygon in polynomial time using dynamic programming, and (based on this counting algorithm) to generate uniformly random triangulations in polynomial time.[15] However, counting the triangulations of a polygon with holes is #P-complete, making it unlikely that it can be done in polynomial time.[16]
Related objects and problems
[edit]- Both triangulation problems are a special case of triangulation (geometry) and a special case of polygon partition.
- Minimum-weight triangulation is a triangulation in which the goal is to minimize the total edge length.
- A point-set triangulation is a polygon triangulation of the convex hull of a set of points. A Delaunay triangulation is another way to create a triangulation based on a set of points.
- The associahedron is a polytope whose vertices correspond to the triangulations of a convex polygon.
- Polygon triangle covering, in which the triangles may overlap.
- Tiling by polygons, where the goal is to cover the entire plane with polygons of pre-specified shapes.
See also
[edit]References
[edit]- ^ a b c d e Mark de Berg, Marc van Kreveld, Mark Overmars, and Otfried Schwarzkopf (2000), "3: Polygon Triangulation", Computational Geometry (2nd ed.), Springer-Verlag, pp. 45–61, ISBN 3-540-65620-0
{{citation}}: CS1 maint: multiple names: authors list (link) - ^ Pickover, Clifford A. (2009), The Math Book, Sterling, p. 184
- ^ Fournier, Alain; Montuno, Delfin Y. (1984), "Triangulating simple polygons and equivalent problems", ACM Transactions on Graphics, 3 (2): 153–174, doi:10.1145/357337.357341, ISSN 0730-0301, S2CID 33344266
- ^ Toussaint, Godfried T. (1984), "A new linear algorithm for triangulating monotone polygons", Pattern Recognition Letters, 2 (3): 155–158, Bibcode:1984PaReL...2..155T, doi:10.1016/0167-8655(84)90039-4
- ^ Meisters, Gary Hosler (1975), "Polygons have ears", American Mathematical Monthly, 82 (6): 648–651, doi:10.2307/2319703, JSTOR 2319703
- ^ ElGindy, Hossam; Everett, Hazel; Toussaint, Godfried T. (1993), "Slicing an ear using prune-and-search", Pattern Recognition Letters, 14 (9): 719–722, Bibcode:1993PaReL..14..719E, doi:10.1016/0167-8655(93)90141-y
- ^ Tarjan, Robert E.; Van Wyk, Christopher J. (1988), "An O(n log log n)-time algorithm for triangulating a simple polygon", SIAM Journal on Computing, 17 (1): 143–178, CiteSeerX 10.1.1.186.5949, doi:10.1137/0217010, MR 0925194
- ^ Kirkpatrick, David G.; Klawe, Maria M.; Tarjan, Robert E. (1992), "Polygon triangulation in O(n log log n) time with simple data structures", Discrete & Computational Geometry, 7 (4): 329–346, doi:10.1007/BF02187846, MR 1148949
- ^ Clarkson, Kenneth L.; Tarjan, Robert; van Wyk, Christopher J. (1989), "A fast Las Vegas algorithm for triangulating a simple polygon", Discrete & Computational Geometry, 4 (5): 423–432, doi:10.1007/BF02187741
- ^ a b Seidel, Raimund (1991), "A Simple and Fast Incremental Randomized Algorithm for Computing Trapezoidal Decompositions and for Triangulating Polygons", Computational Geometry, 1: 51–64, CiteSeerX 10.1.1.55.5877, doi:10.1016/0925-7721(91)90012-4
- ^ Clarkson, Kenneth L.; Cole, Richard; Tarjan, Robert E. (1992), "Randomized parallel algorithms for trapezoidal diagrams", International Journal of Computational Geometry & Applications, 2 (2): 117–133, doi:10.1142/S0218195992000081, MR 1168952
- ^ Chazelle, Bernard (1991), "Triangulating a Simple Polygon in Linear Time", Discrete & Computational Geometry, 6 (3): 485–524, doi:10.1007/BF02574703, ISSN 0179-5376
- ^ Amato, Nancy M.; Goodrich, Michael T.; Ramos, Edgar A. (2001), "A Randomized Algorithm for Triangulating a Simple Polygon in Linear Time", Discrete & Computational Geometry, 26 (2): 245–265, doi:10.1007/s00454-001-0027-x, ISSN 0179-5376
- ^ Li, Fajie; Klette, Reinhard (2011), Euclidean Shortest Paths, Springer, doi:10.1007/978-1-4471-2256-2, ISBN 978-1-4471-2255-5
- ^ Epstein, Peter; Sack, Jörg-Rüdiger (1994), "Generating triangulations at random", ACM Transactions on Modeling and Computer Simulation, 4 (3): 267–278, doi:10.1145/189443.189446, S2CID 14039662
- ^ Eppstein, David (2019), "Counting polygon triangulations is hard", Proc. 35nd Int. Symp. Computational Geometry, Leibniz International Proceedings in Informatics (LIPIcs), vol. 129, Schloss Dagstuhl, pp. 33:1–33:17, arXiv:1903.04737, doi:10.4230/LIPIcs.SoCG.2019.33, ISBN 9783959771047, S2CID 75136891
External links
[edit]- Demo as Flash swf, A Sweep Line algorithm.
- Song Ho's explanation of the OpenGL GLU tesselator

