Wikipedia:Reference desk/Archives/Mathematics/2010 February 17
| Mathematics desk | ||
|---|---|---|
| < February 16 | << Jan | February | Mar >> | February 18 > |
| Welcome to the Wikipedia Mathematics Reference Desk Archives |
|---|
| The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages. |
February 17
[edit]Proof for this example on the Lambert W function?
[edit]The Lambert W function has several examples, but only has proof for the first one.
Does anyone have a proof for example 3? —Preceding unsigned comment added by Luckytoilet (talk • contribs) 05:05, 17 February 2010 (UTC)
- By continuity of exponentiation, the limit c satisfies c = zc = ec log z. Rearranging it a bit gives (−c log z)e−c log z = −log z, thus W(−log z) = −c log z, and c = W(−log z)/(−log z). Not quite sure why the example talks about the "principal branch of the complex log function", the branch of log used simply has to be the same one as is employed for the iterated base-z exponentiation in the definition of the limit. Also, note that the W function is multivalued, but only one of its values can give the correct value of the limit (which is unique (or nonexistent) once log z is fixed).—Emil J. 15:04, 17 February 2010 (UTC)
Follow up: the name for the argument of the logarithmic function
[edit]When reading the exponential term ax, one can say "exponentiation - of a - to the exponent n". However, one can also use the explicit name "base" for a, and say: "exponentiation - of the base a - to the exponent n". My question is about whether one can also use any explicit name for x - when reading the logarithmic term logax, i.e. by saying something like: "logarithm - of the blablabla x - to the base a"... HOOTmag (talk) 08:02, 17 February 2010 (UTC)
- I would reckon a correct term would be argument (but this is quiet general as it would apply to any such function/monomial operator). Also note it would most likely be read as "logarithm base a of the argument x" A math-wiki (talk) 08:56, 17 February 2010 (UTC)
- Why have you posted this again? There is an ongoing discussion above. I suggest that the term for the argument of log is just argument and that it's most sensible to say "the logarithm of x to the base a". Why much there be a technical term? —Anonymous DissidentTalk 09:01, 17 February 2010 (UTC)
@A math-wiki, @Anonymous Dissident: Sorry, but just as the function of exponentiation has two arguments: the "base", and the "exponent", so too does the function of logarithm have two arguments: the "base", and the other argument (whose name is still unknown), so I can't see how the term "argument" may solve the problem, without a confusion. The problem is as follows: does the function of logarithm have a technical term for the second argument (not only for the first one), just as the function of exponentiation has a technical term for the second argument (not only for the first one)? HOOTmag (talk) 14:27, 17 February 2010 (UTC)
- I believe you have got your answer. No it has no special name that anyone here knows of. The closest you'll come to a name is argument. Dmcq (talk) 15:05, 17 February 2010 (UTC)
- If you've read my previous section, you've probably realized that the term "argument" can't even be close to answering my question. Also note that I didn't ask whether "it has a special name that anyone here knows of", but rather whether "it has a special name", and I'll be glad if anybody here know of such a name, and may answer me by "yes" (if they know that there is a special name) or by "no" (if they know that there isn't a special name). HOOTmag (talk) 17:50, 17 February 2010 (UTC)
- Er, the "that anyone here knows of" part is inherent in the process of answering questions by humans. People cannot tell you about special names that they do not know of, by the definition of "know". If you have a problem with that, you should ask at the God Reference Desk rather than the Wikipedia Reference Desk.—Emil J. 18:02, 17 February 2010 (UTC)
- If you answer me "I don't know of a special name", then you've replied to the question "Do you know of a special name". If you answer me: "Nobody here knows of a special name", then you've replied to the question: "Does anyone here know of a special name". However, none of those questions was my original question, since I'm not interested in knowing whether anyone here knows of a special name, but rather in knowing whether there is a special name. I'll be glad if anybody here know of such a name, and may answer me by: "yes, there is" (if they know that there is a special name) or by: "no, there isn't" (if they know that there isn't a special name). HOOTmag (talk) 18:22, 17 February 2010 (UTC)
- No one can positively know that there isn't a name. You can't get a better answer than what Dmcq wrote (unless, of course, there is such a name after all).—Emil J. 18:33, 17 February 2010 (UTC)
- I can positively know that there is a special name for each argument of the function of exponentiation (the special names are "base" and "exponent"), and I can also positively know that there isn't a special name for the argument of functions having exactly 67 elements in their domain. HOOTmag (talk) 18:49, 17 February 2010 (UTC)
- Trying to dictate to a reference desk how they should reply to you is not a good idea if you want answers to further questions. Dmcq (talk) 19:44, 17 February 2010 (UTC)
- Dictate? never! I've just said that any answer like "Nobody here knows of a special name" - doesn't answer my original question, which was not: "Does anyone here know of a special name", but rather was: "Is there a special name". As I've already said: "I will be glad if anybody here know of such a name, and may answer me by 'YES' (if they know that there is a special name) or by: 'NO' (if they know that there isn't a special name)".
- Note that - to be "glad" - doesn't mean: to try to dictate... HOOTmag (talk) 20:31, 17 February 2010 (UTC)
- Ah, but there is a special name for the argument of a function that has exactly 67 elements in its domain. Such an argument is called a "septensexagesimand." Erdős used the term in "On the edge-couplet hyperpartitions of uniregular antitransitive trigraphs," J. Comb. Omni. Math. Acad. 61(3):1974, 201–212. —Bkell (talk) 22:26, 17 February 2010 (UTC)
- When you review the article you see that the name was slightly different: "trisexagesimand", and that it was for 63 elements only. As for 67 elements, I know for sure that there's no special name. HOOTmag (talk) 08:27, 18 February 2010 (UTC)
- Oops, sorry, my mistake. —Bkell (talk) 09:00, 18 February 2010 (UTC)
- When you review the article you see that the name was slightly different: "trisexagesimand", and that it was for 63 elements only. As for 67 elements, I know for sure that there's no special name. HOOTmag (talk) 08:27, 18 February 2010 (UTC)
- Trying to dictate to a reference desk how they should reply to you is not a good idea if you want answers to further questions. Dmcq (talk) 19:44, 17 February 2010 (UTC)
- I can positively know that there is a special name for each argument of the function of exponentiation (the special names are "base" and "exponent"), and I can also positively know that there isn't a special name for the argument of functions having exactly 67 elements in their domain. HOOTmag (talk) 18:49, 17 February 2010 (UTC)
- No one can positively know that there isn't a name. You can't get a better answer than what Dmcq wrote (unless, of course, there is such a name after all).—Emil J. 18:33, 17 February 2010 (UTC)
- If you answer me "I don't know of a special name", then you've replied to the question "Do you know of a special name". If you answer me: "Nobody here knows of a special name", then you've replied to the question: "Does anyone here know of a special name". However, none of those questions was my original question, since I'm not interested in knowing whether anyone here knows of a special name, but rather in knowing whether there is a special name. I'll be glad if anybody here know of such a name, and may answer me by: "yes, there is" (if they know that there is a special name) or by: "no, there isn't" (if they know that there isn't a special name). HOOTmag (talk) 18:22, 17 February 2010 (UTC)
- Er, the "that anyone here knows of" part is inherent in the process of answering questions by humans. People cannot tell you about special names that they do not know of, by the definition of "know". If you have a problem with that, you should ask at the God Reference Desk rather than the Wikipedia Reference Desk.—Emil J. 18:02, 17 February 2010 (UTC)
- If you've read my previous section, you've probably realized that the term "argument" can't even be close to answering my question. Also note that I didn't ask whether "it has a special name that anyone here knows of", but rather whether "it has a special name", and I'll be glad if anybody here know of such a name, and may answer me by "yes" (if they know that there is a special name) or by "no" (if they know that there isn't a special name). HOOTmag (talk) 17:50, 17 February 2010 (UTC)
- In an attempt to answer your question in an acceptable manner, I will first note that I (like everyone else here) have never heard a special term for this, but just taking a stab in the dark I searched for "logarithmand" and found that this word has apparently been used at least once in history (though many of the results seem to be false positives resulting from the phrase "logarithm and"). In particular, Martin Ohm used the word in his 1843 book The spirit of mathematical analysis: and its relation to a logical system. So there you are. —Bkell (talk) 09:37, 18 February 2010 (UTC)
- Here are some more usages of the term: George Peacock, 1842, A treatise on algebra; Hermann Schubert and Thomas J. McCormack, 1898, Mathematical Essays and Recreations (in which is also offered the technical term "number"; see also the Project Gutenberg edition); and the German Wikipedia entry on Logarithmus. —Bkell (talk) 09:53, 18 February 2010 (UTC)
- That was quite some stab in the dark, congratulations. I guess that's why my wife is better at crosswords than me :) Dmcq (talk) 11:03, 18 February 2010 (UTC)
- By the way if you like that I'm sure you'll like logarithmancy which is divination using Napier's logarithm tables Dmcq (talk) 11:14, 18 February 2010 (UTC)
- Hahaha… And logarithmandering, the establishment of political boundaries so as to resemble a nautilus shell? —Bkell (talk) 11:27, 18 February 2010 (UTC)
- Oh, wait, you were serious—logarithmancy is actually a real thing. Well, whaddya know. —Bkell (talk) 11:30, 18 February 2010 (UTC)
- Here are some more usages of the term: George Peacock, 1842, A treatise on algebra; Hermann Schubert and Thomas J. McCormack, 1898, Mathematical Essays and Recreations (in which is also offered the technical term "number"; see also the Project Gutenberg edition); and the German Wikipedia entry on Logarithmus. —Bkell (talk) 09:53, 18 February 2010 (UTC)
- Thank you, Bkell, for your discovery! I appreciate that! I think it's a good idea to add this information to the English Wikipedia, (in logarithm). HOOTmag (talk) 12:31, 18 February 2010 (UTC)
- I doubt it is of current interest and wikipedia isn't a dictionary. But it should go in wiktionary I guess if that other word is there. Dmcq (talk) 12:38, 18 February 2010 (UTC)
- As Bkell has pointed out, it is - already - in the German Wikipedia. HOOTmag (talk) 12:54, 18 February 2010 (UTC)
- The use in German has no relevance. Dmcq (talk) 13:12, 18 February 2010 (UTC)
- The use of this term is not just in German, it's in English too, as appearing in the sources Bkell indicated. I mentioned the German Wikipedia - not for showing the German term (since it's a universal term) - but rather for showing that the very information about the special (universal) name for the argument of logarithm appears in other wikipedias as well (not only in wiktionaries). HOOTmag (talk) 13:44, 18 February 2010 (UTC)
- I question your claim that it's a "universal" term. As far as I can see, the term is primarily used in German; the only sources we have in English are from the 19th century, two of which were written by German authors (one of them in the German language, so the translator, lacking an English equivalent, probably just kept the German word) and the last of which only mentions it in a footnote and cites a German work. Yes, it has been used in English, but it is extraordinarily rare and seems to have failed to gain acceptance in any significant way. —Bkell (talk) 13:53, 18 February 2010 (UTC)
- In fact, for what it's worth, during my brief explorations trying to find a term for the argument of the logarithm function, I found more sources that called it the "number" than that called it the "logarithmand" (this includes two of the four sources I gave for "logarithmand"). So if you're going to mention that the argument is sometimes called the logarithmand, you should be honest and also say that it is more commonly called the "number" and even more commonly not called anything at all. —Bkell (talk) 14:00, 18 February 2010 (UTC)
- According to your treatise, the first auther to have used this term is George Peacock (in "A treatise on algebra", 1842), right? His name doesn't sound German... HOOTmag (talk) 14:07, 18 February 2010 (UTC)
- Did you read that link? The term appears in a footnote that ends with, "See Ohm's Versuch eines vollkommen consequenten system der mathematick, Vol. 1." That's why I said, "…the last of which only mentions it in a footnote and cites a German work." —Bkell (talk) 14:13, 18 February 2010 (UTC)
- Even the German wikipedia says it isn't used nowadays. Dmcq (talk) 15:36, 18 February 2010 (UTC)
- Did you read that link? The term appears in a footnote that ends with, "See Ohm's Versuch eines vollkommen consequenten system der mathematick, Vol. 1." That's why I said, "…the last of which only mentions it in a footnote and cites a German work." —Bkell (talk) 14:13, 18 February 2010 (UTC)
- According to your treatise, the first auther to have used this term is George Peacock (in "A treatise on algebra", 1842), right? His name doesn't sound German... HOOTmag (talk) 14:07, 18 February 2010 (UTC)
- The use of this term is not just in German, it's in English too, as appearing in the sources Bkell indicated. I mentioned the German Wikipedia - not for showing the German term (since it's a universal term) - but rather for showing that the very information about the special (universal) name for the argument of logarithm appears in other wikipedias as well (not only in wiktionaries). HOOTmag (talk) 13:44, 18 February 2010 (UTC)
- The use in German has no relevance. Dmcq (talk) 13:12, 18 February 2010 (UTC)
- As Bkell has pointed out, it is - already - in the German Wikipedia. HOOTmag (talk) 12:54, 18 February 2010 (UTC)
- I doubt it is of current interest and wikipedia isn't a dictionary. But it should go in wiktionary I guess if that other word is there. Dmcq (talk) 12:38, 18 February 2010 (UTC)
- Thank you, Bkell, for your discovery! I appreciate that! I think it's a good idea to add this information to the English Wikipedia, (in logarithm). HOOTmag (talk) 12:31, 18 February 2010 (UTC)
First/second order languages
[edit]- How should we call a first/second order language, whose all symbols are logical (like connectives quantifiers variables and brackets and identity), i.e. when it contains neither constants nor function symbols nor predicate symbols (but does contain the identity symbol)?
- If a given open well-formed formula contains signs of variables ranging over individuals, as well as signs of variables ranging over functions, while all quantifications are used therein over variables ranging over individuals only (hence without quantifications over variables ranging over functions), then: is it a first order formula, or a second order formula?
- Note that such open formulae can be used (e.g.) for defining correspondences (e.g. bijections) between classes of functions (e.g. by corresponding every invertible function to its inverse function).
HOOTmag (talk) 17:53, 17 February 2010 (UTC)
- I'm a novice so I'm not sure if my answers are correct. Your 1st question: if there are no predicate symbols, there would be no atomic formulas and hence no wfs. Your 2nd question: it a second order formula because first order can only have variables over the universe of discourse. Your note: I think function are coded as sets in set theories, hence defining a bijection would be a 1st order formula because variables/quantifies are over sets (the objects in our domain). Money is tight (talk) 18:12, 17 February 2010 (UTC)
- There are plenty of formulas in languages without nonlogical symbols. In first-order logic, apart from , (if they are included in the particular formulation of first-order logic) you have also atomic formulas using equality, and therefore the language is sometimes called the "language of pure equality". In second-order logic, there are also atomic formulas using predicate variables. One could probably call it the language of pure equality as well, but there is little point in distinguishing it: any formula in a richer language may be turned into a formula without nonlogical symbols by replacing all predicate and function symbols with variables (and quantifying these away if a sentence is desired). As for the second question, the formula is indeed a second-order formula, but syntactically it is pretty much indistinguishable from the first-order formula obtained by reinterpreting all the second-order variables as function symbols.—Emil J. 18:28, 17 February 2010 (UTC)
- Sorry, but I couldn't figure out your following statement:
- any formula in a richer language may be turned into a formula without nonlogical symbols by replacing all predicate and function symbols with variables (and quantifying these away if a sentence is desired).
- Realy? If I use a richer language, containing a function symbol - which (in a given model) receives a colour and returns it's negative colour, so how can I replace that function symbol by a function variable without losing my original interpretation for the function?
- HOOTmag (talk) 13:02, 18 February 2010 (UTC)
- Sorry, but I couldn't figure out your following statement:
- There are plenty of formulas in languages without nonlogical symbols. In first-order logic, apart from , (if they are included in the particular formulation of first-order logic) you have also atomic formulas using equality, and therefore the language is sometimes called the "language of pure equality". In second-order logic, there are also atomic formulas using predicate variables. One could probably call it the language of pure equality as well, but there is little point in distinguishing it: any formula in a richer language may be turned into a formula without nonlogical symbols by replacing all predicate and function symbols with variables (and quantifying these away if a sentence is desired). As for the second question, the formula is indeed a second-order formula, but syntactically it is pretty much indistinguishable from the first-order formula obtained by reinterpreting all the second-order variables as function symbols.—Emil J. 18:28, 17 February 2010 (UTC)
- A language is entirely syntactic, it does not include an interpretation, which is a separate matter. Emil is saying that the formula "a - b" can be viewed either as a first-order formula with a function symbol "-" and free variables a and b, or as a second-order formula with variables a and b of type 0 and a free variable "-" of higher type. The formula, being just a string of symbols, does not know whether "-" is meant to be a function symbol or a function variable. The same holds for the "=" predicate, actually. — Carl (CBM · talk) 13:36, 18 February 2010 (UTC)
- The atomic formula "x=x" has no non-logical predicate symbols (note that the identity sign is logical): all of its symbols are logical (including the symbol of identity)
- Note that the universe of discourse is the set of individuals and of functions ranging over those individuals.
- HOOTmag (talk) 18:35, 17 February 2010 (UTC)
- A first order theory with equality is one that has a predicate symbol that also has axioms of reflexivity and substitutivity. I'm not sure why you say x=x has no non logical symbols. Clearly the only logical connectives are for all, there exist, not, or, and, material implication. And the universe of discourse only contains the individuals D in our question, not functions with domain D^n. The functions are called 'terms', which are used to build atomic formulas and then wfs. Money is tight (talk) 18:43, 17 February 2010 (UTC)
- In first-order logic with equality, the equality symbol is considered a logical symbol, the reason being that its semantics is fixed by the logic (in a model you are not allowed to assign it a binary relation of your choice, it's always interpreted by the identity relation). Anyway, the OP made it clear that he intended the question that way, so it's pointless to argue about it.—Emil J. 19:24, 17 February 2010 (UTC)
- @Money is tight: Your comment regarding the domain of discourse is correct. Sorry for my mistake. HOOTmag (talk) 13:13, 18 February 2010 (UTC)
- The contents of the domain(s) of discourse will depend on what semantics are used. See second-order logic for an explanation. — Carl (CBM · talk) 13:24, 18 February 2010 (UTC)
- A first order theory with equality is one that has a predicate symbol that also has axioms of reflexivity and substitutivity. I'm not sure why you say x=x has no non logical symbols. Clearly the only logical connectives are for all, there exist, not, or, and, material implication. And the universe of discourse only contains the individuals D in our question, not functions with domain D^n. The functions are called 'terms', which are used to build atomic formulas and then wfs. Money is tight (talk) 18:43, 17 February 2010 (UTC)
Note that in higher-order languages for arithmetic, equality of higher types is very often not taken as a logical symbol.
In the context of higher-order arithmetic, a formula with no higher-order quantifiers (but possibly higher-order variables) is called "arithmetical". For example, the formula is an arithmetical formula with a free variable F of type 0→0.
As for "first-order languages" versus "second-order languages", this distinction breaks down upon closer inspection. One cannot tell which semantics are being used merely by looking at syntactic aspects of a formula, and so the very same syntactical language can be both a first-order language and a second-order language. The language of the theory named second-order arithmetic is an example of this: the usual semantics for this theory are first-order semantics, and so in that sense the language is a first-order language (with two sorts).
However, classical usage has led to several different informal meanings for "higher-order language" in the literature, which are clear to experts but not formally defined. — Carl (CBM · talk) 13:23, 18 February 2010 (UTC)
Homomorphism
[edit]I'm looking for two homomorphisms f:S2->S3, g:S3->S2 such that the composition gf is the identity on S2 (the S means the 2nd and 3rd symmetric groups). Does two such homomorphism exist? I know everything is finite so I can brute force my way but I don't like that approach. Thanks Money is tight (talk) 18:00, 17 February 2010 (UTC)
- If gf is the identity, then g is a surjection. Thus its kernel must be a normal subgroup of index 2. Can you find one? This will give you g, and then constructing the matching f should be easy.—Emil J. 18:14, 17 February 2010 (UTC)
- Perhaps I am confused; wouldn't the kernel of g need to have index 3? Eric. 131.215.159.171 (talk) 23:21, 17 February 2010 (UTC)
- Yes, you're confused. The index of the kernel is the same as the order of the image. Perhaps you're confusing index with order? Algebraist 23:24, 17 February 2010 (UTC)
- You're right, I am confused. My thoughts were S2 has order 2, S3 has order 6, so "index" is 3... oops. Eric. 131.215.159.171 (talk) 00:29, 18 February 2010 (UTC)
- Yes, you're confused. The index of the kernel is the same as the order of the image. Perhaps you're confusing index with order? Algebraist 23:24, 17 February 2010 (UTC)
- Perhaps I am confused; wouldn't the kernel of g need to have index 3? Eric. 131.215.159.171 (talk) 23:21, 17 February 2010 (UTC)
It may be helpful to analyze this problem more generally: For which m and n do there exist homomorphisms and such that the composition is the identity on ? If you use EmilJ's method, you should solve this general problem; however, it might also be necessary to precisely determine the normal subgroups of for all natural x (and this is not too hard to do if you are equipped with the right theorems). PST 01:10, 18 February 2010 (UTC)
- Let H be the subgroup consisting of e, k1, k2, where e is the identity and k1 k2 are the two elements with each other as inverse (for example k1 is the function f(1)=2, f(2)=3, f(3)=1). I think this is the subgroup EmilJ is to talking about. Now map everything in H to the identity i in S2, and the rest to the other element in S2. I think this is a homomorphism g. Then define f to be the map that sends i to e and the other element in S2 to one of the three elements in S3 with itself as inverse. Correct? Money is tight (talk) 06:09, 18 February 2010 (UTC)
- Correct. You might like to see the article alternating group; every non-trivial permutation group has a unique subgroup of index 2, and this is referred to as the alternating group (perhaps more concretely, an element of is in if and only if it is the product of an even number of transpositions). Using your notation, the alternating subgroup , the unique subgroup of with index 2, is simply . There are other useful results about alternating groups that can help you to solve generalizations of this problem; for instance, is normal in for all natural n (since, of course, any subgroup of index 2 in a group must be normal). Therefore, if we define by setting g to be the identity of for all elements in , and the (unique) non-identity element of for all elements outside , g is a homomorphism on with kernel . If we define by setting f to be an element of order 2 outside on the (unique) non-identity element of , and the identity element of on the identity of , f is also a homomorphism and is the identity on . In case you are studying permutation groups at the moment (are you?), you might find this interesting. PST 08:49, 18 February 2010 (UTC)
- You are probably already aware of this, but it may also help to explicitly write down the elements of : where we use cycle notation to describe the individual elements. Of course, this will become too cumbersome should we investigate higher order permutation groups, and thus the above method (described by EmilJ) is more appropriate. PST 08:58, 18 February 2010 (UTC)
- Correct. You might like to see the article alternating group; every non-trivial permutation group has a unique subgroup of index 2, and this is referred to as the alternating group (perhaps more concretely, an element of is in if and only if it is the product of an even number of transpositions). Using your notation, the alternating subgroup , the unique subgroup of with index 2, is simply . There are other useful results about alternating groups that can help you to solve generalizations of this problem; for instance, is normal in for all natural n (since, of course, any subgroup of index 2 in a group must be normal). Therefore, if we define by setting g to be the identity of for all elements in , and the (unique) non-identity element of for all elements outside , g is a homomorphism on with kernel . If we define by setting f to be an element of order 2 outside on the (unique) non-identity element of , and the identity element of on the identity of , f is also a homomorphism and is the identity on . In case you are studying permutation groups at the moment (are you?), you might find this interesting. PST 08:49, 18 February 2010 (UTC)
Ominus
[edit]What's the conventional meaning and usage of the symbol encoded by the LaTeX markup "\ominus"? (i.e. ). There doesn't currently seem to be a ominus Wikipedia page yet. -- 140.142.20.229 (talk) 18:50, 17 February 2010 (UTC)
- Mainly this: if are closed linear subspaces of a Hilbert space, denotes the orthogonal subspace of relative to , that is . It comes of course from the notation for the orthogonal sum, As you see, it doesn't seem so theoretically relevant to deserve an article of its own; but as a notation is nice and of some use. --pma 19:08, 17 February 2010 (UTC)
- It is also used in loads of other places like removing parts of a graph or when reasoning about computer floating point where there is a vaguely subtraction type of operator and the person wants a symbol for it. Basically a generally useful extra symbol. Dmcq (talk) 19:36, 17 February 2010 (UTC)
- Note that "ominus" isn't meant to be a single word; it's meant to be read as "O minus", suggesting a minus sign within an O. Likewise there are \oplus , \otimes , \odot , etc. The official term for the symbol, if there is one, is probably something like "circled minus sign"; but \ominus is shorter to type, and that's what Knuth called it when he wrote TeX. —Bkell (talk) 07:47, 18 February 2010 (UTC)
- The respective Unicode 5.2 character code chart Mathematical Operators calls it "CIRCLED MINUS" (code point 2296hex). —Tobias Bergemann (talk) 09:27, 18 February 2010 (UTC)
Spherical harmonic functions
[edit]I'm looking for the normal modes of a uniform sphere. I have a classic text on solid mechanics, by A. E. H. Love, but I can't quite make sense of the math. He gives a formula for the mode shape in terms of "spherical solid harmonics" and "spherical surface harmonics," which he uses and discusses in a way that doesn't seem to match Wikipedia's description of spherical harmonics. Can you help me identify these functions? The following facts seem to be important:
- The general case of a "spherical solid harmonic" is denoted . Note the presence of only one index, rather than two.
- , where is a "spherical surface harmonic." I would expect S to be equivalent to Y, except that it's missing one index.
- Unlike the regular spherical harmonics Y, the "spherical solid harmonics" V apparently come in many classes, three of which are important to his analysis and denoted , , and . The description of the distinction between these classes makes zero sense to me.
- Several vector-calculus identities involving V are given. I can type these up if anyone wants to see them.
Does anyone know what these functions V or S are? --Smack (talk) 18:59, 17 February 2010 (UTC)
- S is surely just Y with and the m index suppressed (perhaps azimuthal variations are less important here?), which makes V a (regular) solid harmonic R with the same index variations. I don't know what the classes of solid harmonics are supposed to be, unless he's denoting the different values of m as different classes (0 and ±1, or 0/1/2?). --Tardis (talk) 20:51, 17 February 2010 (UTC)
- Thanks; that answers my question except for the problem of the missing m index. I can't see why azimuthal variation would be less important, since the subject is the mechanics of a sphere. Thinking out loud for a minute, I can come up with the following possibilities:
- According to your guess, the three classes correspond to m = 0, ±1, ±2. In this case, I would expect to find an equation using ω, and be able to substitute φ or χ to get a different mode. However, the mode shape equation uses both ω and φ, which makes substitution difficult.
- m can take any arbitrary value (). This makes no sense in light of the frequency equation, which has n all over it (as it should), but does not use any other index (which it also should).
- m is fixed to a single value, most likely or . This would be silly in a text claiming to discuss all of the modes of a sphere. (The original work was published in 1882. Surely both indices of the Y function had been discovered by then?)
- --Smack (talk) 22:34, 17 February 2010 (UTC)
- Thanks; that answers my question except for the problem of the missing m index. I can't see why azimuthal variation would be less important, since the subject is the mechanics of a sphere. Thinking out loud for a minute, I can come up with the following possibilities:
math conversion two
[edit]is there a website where I can convert litre into mililitre, convert litre into pint, convert into gallon, convert litre into kilogram, litre into decalitre and such? —Preceding unsigned comment added by 74.14.118.209 (talk) 20:22, 17 February 2010 (UTC)
- Google will do most of that for you, e.g. type "2 litres in pints". Litre to kilogram though would be dependent on the density of what you are measuring. Note that some of your conversions are simply multiplication or division based on the prefix (litre to millilitre, for example). --LarryMac | Talk 20:32, 17 February 2010 (UTC)
- For anything beyond Google's capabilities, check out Online Conversion. --Smack (talk) 22:36, 17 February 2010 (UTC)
- Be aware that there are different kinds of pints, gallons, etc. Google assumes by default that you want US liquid measure; if you want Imperial, you have to say "2 liters in imperial pints" or similar. Or perhaps this depends on what country it thinks you are in. Similar issues arise with other units, such as tons. --Anonymous, 06:19 UTC, December 18, 2010.
- No need to go to a website. Just pull up an xterm and run units. 58.147.58.28 (talk) 10:21, 18 February 2010 (UTC)
Minkowski paper on L1 distance
[edit]I know that L1 distance is often referred to as Minkowski distance. I'm trying to find out where (in which paper/book) did Minkowski introduce L1 distance. I can only find many references stating that he introduced the topic, but no references to a specific paper or book. Does anyone here know the name of the paper/book? -- kainaw™ 20:59, 17 February 2010 (UTC)
- Looked around, and also found it was a frustrating question to find out directly, could only find at best references to his collected works, implying a trip to the library, sooo second millennium. So guess/vague memory that it was from his Geometry of numbers led to this nice paper or [1], with this ref: H. Minkowski, Sur les propriétés des nombres entiers qui sont dérivées de l’intuition de l’espace, Nouvelles Annales de Mathematiques, 3e série 15 (1896), Also in Gesammelte Abhandlungen, 1. Band, XII, pp. 271–277. Also mentions that Riemann mentioned L4 in his famous Habilitationsschrift.John Z (talk) 01:55, 19 February 2010 (UTC)
- Thanks. I also went to the library and was directed to a German copy of "Raum und Zeit", which appears to be a collection of his talks on L-space. I found a German copy online and used Babelfish to make sense of it - which wasn't too bad considering it is a physics/math book. -- kainaw™ 02:00, 19 February 2010 (UTC)
- Thanks again - the history section of that first paper is great. -- kainaw™ 02:02, 19 February 2010 (UTC)
LaTeX matrices
[edit]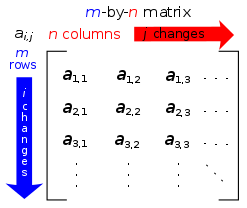
Is there any way of creating matrices in LaTeX where you display the name of each individual row and column on the left and top of the matrix respectively? Drawing an adjacency matrix would look something like this:
| Labeled graph | Adjacency matrix |
|---|---|
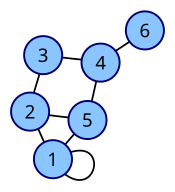
|
only with on the top of the matrix and the same on it's side- because the matrix doesn't say which vertices of the graph relates to which row or column in it's current state. Is this an odd request? I could have sworn I've seen people do this (especially when the names of the vertices are odd) --BiT (talk) 21:46, 17 February 2010 (UTC)
- One way to do something somewhat similar:
- or in two dimensional case:
- It only looks reasonably nice in case of a one-dimensional array, but it's still better than nothing... --Martynas Patasius (talk) 22:57, 17 February 2010 (UTC)
- In plain TeX there is a macro called
\bmatrix\bordermatrix that will do what you want. Searching for latex bordermatrix will hopefully lead you to something. —Bkell (talk) 07:53, 18 February 2010 (UTC)- Thank you very much Bkell, that was exactly what I was looking for. --BiT (talk) 15:29, 18 February 2010 (UTC)
- In plain TeX there is a macro called
Integral of 1/x
[edit]User:Daqu mentioned a problem with the usual expression for the real number integral of 1/x on the page Talk:Range (mathematics). The usual answer is
The problem I see is if someone integrates over an interval including 0. Should one just say the value is indeterminate, use the complex logarithm, or just accept that people might come up with 0 when integrating between −1 and +1? after all one might consider the two areas as canceling even if they are both infinite! Has anyone seen a book that actually mentions this problem? Dmcq (talk) 22:44, 17 February 2010 (UTC)
- You can't integrate right through 0 even in the complex case, I'm pretty sure, at least without getting into careful analysis of what kind of integral you mean (e.g. the Henstock-Kurzweil integral might be able to handle it). Of course the contour integral is well-defined for any other path, with the Cauchy integral formula describing what happens for closed loops around the origin. 66.127.55.192 (talk) 23:47, 17 February 2010 (UTC)
- Technically the above formula is an indefinite integral and really all it says is that the derivative of is , with the restriction x ≠ 0 implicit from the domains of the functions involved. What you're really saying is that there is a problem when you try to apply the fundamental theorem of calculus with this formula, but the conditions required for the FTC would eliminate cases where the interval of integration is not a subset of the domain, as would be the case here. So actually everything is correct here but if I was teaching a calculus class I would be careful to point out to students that due care is needed when applying this formula.--RDBury (talk) 00:00, 18 February 2010 (UTC)
- So just add a warning about not integrating at 0, sounds good to me. Thanks Dmcq (talk) 01:01, 18 February 2010 (UTC)
- One of the basic properties of the Henstock–Kurzweil integral is that whenever exists, then exists for any a ≤ c ≤ d ≤ b as well. Thus 1/x is not Henstock–Kurzweil integrable over any interval containing 0. As far as I can see, the only way to make the integral converge is to use the Cauchy principal value.—Emil J. 13:50, 18 February 2010 (UTC)
- Is it an indefinite integral? At the freshman level, one makes no distinction between indefinite integrals and antiderivatives, but is that the right level for the context? Michael Hardy (talk) 04:03, 18 February 2010 (UTC)
The integral in question does have a Cauchy principal value.
I have an issue with the assertion that
if that is taken to identify all antiderivatives. It should say
Michael Hardy (talk) 03:59, 18 February 2010 (UTC)
- Farly old problem solved before infinitesimals were such a problem. inf-inf=indeterminate or which infinity is greater? The area under 1/x where x<0 or the area under 1/x where x>0? See [[2]] —Preceding unsigned comment added by 68.25.42.52 (talk) 15:34, 18 February 2010 (UTC)
- As I said, there's a Cauchy principal value in this case. And it's 0. Michael Hardy (talk) 03:10, 19 February 2010 (UTC)
Thanks. I've put something at Lists_of_integrals#Integrals_of_simple_functions based on that to see the reaction but I would like a citation. Dmcq (talk) 14:02, 23 February 2010 (UTC)
Consistency of arithmetic Mod N
[edit]The consistency of ordinary arithmetic has not yet been satifactorily settled. What is the upper limit for N such that arithmetic modulo N is known to be consistent? Count Iblis (talk) 23:55, 17 February 2010 (UTC)
(Sorry, messed up the page history somehow. Eric. 131.215.159.171 (talk) 00:01, 18 February 2010 (UTC))
- I think you need to specify what framework you want to consistency to be proven within. However, if you can prove it for any N I would expect you can prove it for all N. --Tango (talk) 00:03, 18 February 2010 (UTC)
- Arithmetic mod N has a finite model so in principle you can check the axioms against it directly. Whether the consistency of arithmetic is settled is of course subject to debate, but Gentzen's consistency proof (using what amounts to structural induction on formulas, don't flip out at the term "transfinite induction" since there are no completed infinities involved) and Gödel's functional proof (which does use infinitistic objects of a limited sort) are both generally accepted. 66.127.55.192 (talk) 01:15, 18 February 2010 (UTC)
- You didn't specify what axiom system for arithmetic modulo n you have in mind, and you didn't specify the power of your metatheory. As for the axiomatization, Th(A) is finitely axiomatizable for any finite model A in a finite language, so let me just assume that you fix any finite complete axiomatization Zn of Th(Z/nZ) in the (functionally complete, in this case) language of rings (the particular choice of the axioms does not matter, since the equivalence of two finitely axiomatized theories is a -statement, and is thus verifiable already in Robinson arithmetic whenever it is true).
- Now, what metatheory suffices to prove the consistency of Zn? In the case n = 2, Z2 is a notational variant of the quantified propositional sequent calculus, hence questions on its consistency strength belong to propositional proof complexity. The answer is that its consistency is known to be provable in Buss's theory . The proof basically amounts to constructing a truth predicate for QBF, which in turn relies on the fact that the truth predicate is computable in PSPACE. Now, exactly the same argument applies to any fixed finite first-order structure, such as Z/nZ. Thus, proves the consistency of Zn for every fixed n. is a variant of bounded arithmetic, and as such it is interpretable on a definable cut in Robinson's arithmetic Q; thus the consistency proof is finitistic even according to strict standards of people like Nelson. And, in case it is not obvious from the above, the consistency of arithmetic modulo n for each n has nothing to do with the consistency of Peano arithmetic.—Emil J. 15:06, 18 February 2010 (UTC)
- I should also stress that conversely, the power of (or a similar PSPACE theory) is more or less required to prove the consistency of Zn. More precisely, if T is any first-order theory which has no models of cardinality 1 (such as Zn), then over a weak base theory the consistency of T implies the consistency of the quantified propositional sequent calculus, which in turn implies all -sentences provable in (note that consistency statements are themselves ).—Emil J. 16:10, 18 February 2010 (UTC)



















































