Wikipedia:Reference desk/Archives/Science/2020 January 31
| Science desk | ||
|---|---|---|
| < January 30 | << Dec | January | Feb >> | February 1 > |
| Welcome to the Wikipedia Science Reference Desk Archives |
|---|
| The page you are currently viewing is a transcluded archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages. |
January 31
[edit]Triple point of water
[edit]Is a slush of ice in water an example of water at it's triple point? We clearly have both solid and liquid water present, and the vapor pressure of water will certainly be non-zero, so doesn't that fulfill the criteria of being at the triple point (having 3 phases present together)? Am I correct to assume that the temperature of the slush and the vapor pressure will tend to the triple point values for water (0.01°C and 0.006atm)? 139.194.157.157 (talk) 11:11, 31 January 2020 (UTC)
- Your example demonstrates the coexistence of solid and liquid phases at 1 atmosphere pressure, and a temperature slightly lower than that of the triple point. Dolphin (t) 11:24, 31 January 2020 (UTC)
- No, to be at the triple point, the phases have to be more than just coexisting at the time. They need to be in equilibrium, which is to say that if left alone, they need to remain at the same relative amounts. If you leave your mixture for an extended period of time, if the water is evaporating or if the ice is melting in the slush, it is not at equilibrium. If you come back in an hour, and some of the ice has melted, you were not at equilibrium and you were thus not at the triple point. The triple point is defined by this behavior, so you actually have to have a temperature of exactly 0.01 deg C and 0.006 atm. You also need to have a system which is at thermodynamic equilibrium, which is to say it is a closed system with no internal temperature or pressure gradients, thus the entire container holding the ice, water, and vapor would need to be at 0.01 degrees C and 0.006 atm, and well insulated from its surroundings. At room pressure and room temperature, you are NOT at those conditions. --Jayron32 14:31, 31 January 2020 (UTC)
- The above is correct except for
if the water is evaporating
. There is a subtle difference between evaporation and boiling. Evaporation: for any condition (temperature/pressure/etc.) where liquid is present, there will be a small but nonzero amount of gas phase; at equilibrium its partial pressure is equal to the vapor pressure. Boiling: the liquid phase can be less stable from an enthalpy point of view, and completely transform into the gas phase, depending on the temperature and (total, not partial) pressure. Boiling is what defines the triple point. TigraanClick here to contact me 14:52, 31 January 2020 (UTC)- Yes, of course. Thanks for the correction. --Jayron32 17:40, 31 January 2020 (UTC)
- Boiling happens when the vapour pressure equals that of the ambient atmosphere. So, there is no connection between the boiling of water and the triple point. Ruslik_Zero 19:53, 1 February 2020 (UTC)
- See Triple point of water which is a stable equilibrium that occurs only at 0.0075 °C and 0.00603659 atm. That is the minimum pressure at which liquid water can exist. DroneB (talk) 15:53, 31 January 2020 (UTC)
- The above is correct except for
String vibratio
[edit]A string is stretched between two supports such as the bridge and nut of a guitar. If the fundamental frequency sting is f, ant what frequncy doesc the bridge (or nit) vibrate, and why?86.8.201.66 (talk) 14:36, 31 January 2020 (UTC)
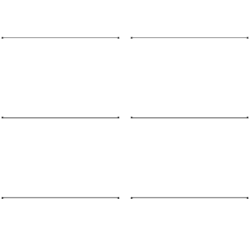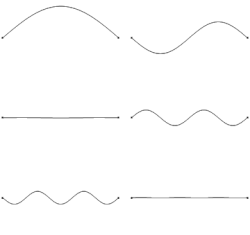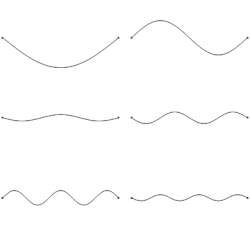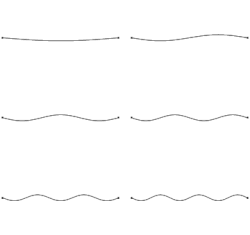
- The diagram shows the string vibration frequency components. Their relative amplitudes vary depending on where the string was plucked: for a clear musical note pluck at the center of the string, for a "tinny" sound that is mostly high harmonics pluck near either end of the string. On a Guitar (see article) the upper end support is either the nut (open string) or a fret chosen by the player's finger. The lower end support is the bridge which on an acoustic guitar is mounted on a flexible soundboard that couples the string vibrations to the surrounding air, producing sound. An electric guitar instead relies on one or more magnetic pickup(s) to convert the vibrations of its steel strings via electronic amplification to sound. Different pickup positions along the strings give sounds with different harmonic content. The initial "attack" sound of a plucked guitar string is a burst of many frequency components as the mechanical impulse travels away from the pluck position and it is subsequent reflection of the impulse from the end supports that augments the standing wave frequencies shown. DroneB (talk) 15:33, 31 January 2020 (UTC)
- If you pluck the center of the string, won't you get a wave with no even components (like an ideal woodwind)? —Tamfang (talk) 07:22, 4 February 2020 (UTC)
- No, generally, you need to dampen the string by lightly touching after striking. You can create pinch harmonics that way by allowing the thumb holding the pick hand to barely touch the string after the plectorum strikes it. It's a rather advanced electric guitar technique. Normal picking produces the normal harmonic series, though where you strike will slightly change the harmonic character by accentuating certain notes in the series, and slightly dampening others as described above. To completely "deaden" an entire set of components of the series requires a more deliberate muting using the skin of your finger after plucking.--Jayron32 19:11, 4 February 2020 (UTC)
- (ec) Almost. An acoustic guitar supports its strings asymmetrically because the nut or fret is solid while the bridge+soundboard flex slightly, so the plucking position for minimum even harmonics is slightly off-centre, but center on a solid bodied electric guitar. However no woodwind can duplicate the harsh attack of a guitar note or its characteristic decay. DroneB (talk) 19:23, 4 February 2020 (UTC)
- If you pluck the center of the string, won't you get a wave with no even components (like an ideal woodwind)? —Tamfang (talk) 07:22, 4 February 2020 (UTC)
- no I'm interested in the cyclical variation in forces on the bridge, by which the sound is transmitted to the body. At what frequency are these forces?
86.8.201.66 (talk) 18:06, 31 January 2020 (UTC)
- They are at the same frequencies as the vibrating string. --Lambiam 18:38, 31 January 2020 (UTC)
- Show me how and why please.86.8.201.66 (talk) 21:04, 31 January 2020 (UTC)
- If you look at the shape of the vibrating string you'll see near the bridge it is operating at an angle. The string has a tension in it, so it is applying a force at that frequency to the bridge. The vertical component will be T*sin(theta) where theta is the angle of the string to the bridge, zero being flat. There may be other effects. Greglocock (talk) 05:08, 1 February 2020 (UTC)
- Show me how and why please.86.8.201.66 (talk) 21:04, 31 January 2020 (UTC)
- They are at the same frequencies as the vibrating string. --Lambiam 18:38, 31 January 2020 (UTC)
- For the how and why, see Vibration#Forced vibration with damping: "The result states that the mass [that is, the body. --L.] will oscillate at the same frequency, f, of the applied force [by the vibrating string. --L.], but with a phase shift " This is a somewhat simplistic model, but if you look at the section Multiple degrees of freedom systems and mode shapes further down, the generic solution implies that all components vibrate with a combination of vibrations at the same set of frequencies (found by the eigenvalues of the equation). If the string vibrates at a combination of multiples of some fundamental, the harmonics, then so will the neck, bridge and soundboards, with the same fundamental. The higher partials need in fact not be perfect harmonics, but if the guitar has a nice sound to it, they are apparently close. --Lambiam 09:55, 1 February 2020 (UTC)
- Doesnt the applied force on the bridge have two maxima per cycle of fundamental string vibration thereby causing a frequency doubling effec4? Or am I missing something?
80.2.20.243 (talk) 16:06, 3 February 2020 (UTC)
- A cycle consists of two maxima in opposite directions. DroneB (talk) 19:05, 4 February 2020 (UTC)
- Yes, for the tension forces, there's a frequency doubling. Which is interesting, particularly for harps.
- I have no explanation for any of this. Nor, it turns out, do any of the luthiers I know. Although I was recommended to Benaud's Fundamentals of Musical Acoustics and also a couple of old SciAm articles Physics of the bowed string - John C Shelling, Jan 1974 and The Physics of Violins - C M Hutchins, Nov 1962. Andy Dingley (talk) 21:34, 4 February 2020 (UTC)
- Great! At last we have two people who are understanding what I've been questioning. This effect, in my view has a fundamental significance as to the production of sound in stringed instruments utilising a bridge.
The doubling frequency mechanism is, in my view, very important in explaining some of the ounter intuitive characteristics of the aforementioned instruments. What we need is some scientific paper that discusses this so the theory can be included in wikimania onvthe appropriate pages. In my searches do far, I have found nothing. Maybe others can find something scientific on this? 86.8.202.8 (talk) 01:51, 7 February 2020 (UTC)


